If a, b, c, d are in GP, prove that
(i) (b + c)(b + d) = (c + a)(c + a)
(ii)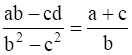 
(iii) (a + b + c + d)2 = (a + b)2 + 2(b + c)2 + (c + d)2
(i) (b + c)(b + d) = (c + a)(c + a)
To prove: (b + c)(b + d) = (c + a)(c + a)
Given: a, b, c, d are in GP
Proof: When a,b,c,d are in GP then
From the above, we can have the following conclusion
⇒ bc = ad … (i)
⇒ b2 = ac … (ii)
⇒ c2 = bd … (iii)
Taking LHS = (b + c)(b + d)
= b2 + bd + bc + cd
Using eqn. (i) , (ii) and (iii)
= ac + c2 + ad + cd
= c(a + c) + d(a + c)
= (a + c) (c + d)
Hence Proved
(ii) 
To prove: 
Given: a, b, c, d are in GP
Proof: When a,b,c,d are in GP then
From the above, we can have the following conclusion
⇒ bc = ad … (i)
⇒ b2 = ac … (ii)
⇒ c2 = bd
⇒ d = 
… (iii)
Taking LHS = 
= 
[From eqn. (iii)]
= 
= 
= 
= 
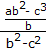
[From eqn. (ii)]
= 
= 
= 
= 
= RHS
Hence Proved
(iii) (a + b + c + d)2 = (a + b)2 + 2(b + c)2 + (c + d)2
To prove: (a + b + c + d)2 = (a + b)2 + 2(b + c)2 + (c + d)2
Given: a, b, c, d are in GP
Proof: When a,b,c,d are in GP then
From the above, we can have the following conclusion
⇒ bc = ad … (i)
⇒ b2 = ac … (ii)
⇒ c2 = bd … (iii)
Taking LHS = (a + b + c + d)2
⇒ (a + b + c + d) (a + b + c + d)
⇒ a2 + ab + ac + ad + ba + b2 + bc + bd + ca + cb + c2 + cd + da + db + dc + d2
On rearranging
⇒ a2 + ab + ba +b2 + ac + ad + bc + bd + ca + cb + c2 + cd + da + db + dc + d2
On rearranging
⇒ (a + b)2 + ac + ad + bc + bd + ca + cb + da + db + c2 + cd + dc + d2
On rearranging
⇒ (a + b)2 + ac + ad + bc + bd + ca + cb + da + db + (c + d)2
On rearranging
⇒ (a + b)2 + ac + ca + ad + bc + cb + da + bd + db + (c + d)2
Using eqn. (i)
⇒ (a + b)2 + ac + ca + bc + bc + bc + bc + bd + db + (c + d)2
Using eqn. (ii)
⇒ (a + b)2 + b2 + b2 + bc + bc + bc + bc + bd + db + (c + d)2
Using eqn. (iii)
⇒ (a + b)2 + 2b2 + 4bc + c2 + c2 + (c + d)2
On rearranging
⇒ (a + b)2 + 2b2 + 4bc + 2c2 + (c + d)2
⇒ (a + b)2 + 2[b2 + 2bc + c2 ] + (c + d)2
⇒ (a + b)2 + 2(b + c)2 + (c + d)2
= RHS
Hence proved