In the given question we need to find the sum of the series.

For that, first, we need to find the n^th term of the series so that we can use summation of the series with standard identities and get the required sum.

The series given is 5 + 7 + 13 + 31 + 85 + …. + n terms.

This question can be solved by the method of difference.

Note:

Consider a sequence a₁, a₂, a₃ …such that the Sequence a₂ –a₁, a₃ – a₂… is either an. A.P. or a G.P.

The n^th term, of this sequence, is obtained as follows:

S = a₁ + a₂ + a₃ +…+ a_n–1 + a_n→ (1)

S = a₁ + a₂ +…+ a_n–2 + a_n–1 + a_n → (2)

Subtracting (2) from (1),

We get, a_n = a₁+ [(a₂–a₁) + (a₃–a₂) +… (a_n – a_n–1)].

Since the terms within the brackets are either in an A.P. or a G.P, we can find the value of a_n, the n^th term.

Thus, we can find the sum of the n terms of the sequence as,

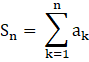
So,

By using the method of difference, we can find the n^th term of the expression.

S_n = 5 + 7 + 13 + 31 + 85 + ….. + a_n→ (1)

S_n = 5 + 7 + 13 + 31+ 85 + …. + a_n→ (2)

(1) – (2) → 0 = 5 + 2 + 6 + 18 + 54+ …..+ (a_n – a_n-1) - a_n

So, n^th term of the series,

a_n = 5 + 2 + 6 + 18 + 54 + ….

In the resulting series obtained, starting from 2, 6, 18…forms a GP.

So, the n^th term forms a GP, with the first term, a = 2; common ratio, r = 3.

The required n^th term of the series is the same as the sum of n terms of GP and 5.

The GP is 2 + 6 + 18 + 54 +… (n-1) terms.

Sum of n terms of a GP,

Sum of (n-1) terms of a GP,

So, n^th term of the series,

Now, we need to find the sum of this series, S_n.

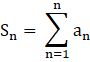
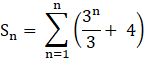
Note:

I. Sum of first n natural numbers, 1 + 2 +3+…n,

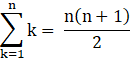
II. Sum of squares of first n natural numbers, 1² + 2² + 3²+….n²,

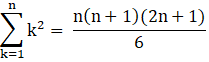
III. Sum of cubes of first n natural numbers, 1³ + 2³ + 3³ +…..n³,

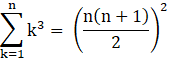
IV. Sum of a constant k, N times,

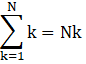
So, for the given series, we need to find,

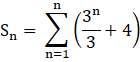
From, the above identities,

→ (a)

The first term in (a) is a GP, with the first term, a = 3 and common ratio, r = 3.

Sum of n terms of GP,

So, Sum of the series,