If 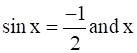 lies in Quadrant IV, find the values of
lies in Quadrant IV, find the values of
(i) 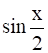 (ii)
(ii) 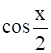
(iii) 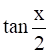
Given: sin x = ![]() and x lies in Quadrant IV.
and x lies in Quadrant IV.
To Find: i)sin ![]() ii)cos
ii)cos ![]() iii)tan
iii)tan ![]()
Now, since sin x = ![]()
We know that cos x = ![]()
cos x = ![]()
cos x = ![]()
cos x = ![]()
since cos x is positive in IV quadrant, hence cos x = ![]()
i) sin ![]()
Formula used:
sin ![]() =
= ![]()
Now, sin ![]() =
= 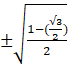 =
= 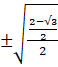 =
= ![]() = =
= = ![]()
Since sinx is negative in IV quadrant, hence sin ![]()
ii)cos ![]()
Formula used:
cos ![]() =
= ![]()
now, cos ![]() =
= 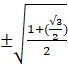 = =
= = 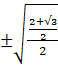 = =
= = ![]()
since cosx is positive in IV quadrant, hence cos ![]() =
= ![]()
iii)tan ![]()
Formula used:
tan x = ![]()
hence, tan ![]() =
= ![]() =
=  =
= ![]() = -1
= -1
Here, tanx is negative in IV quadrant.
1