Differentiate
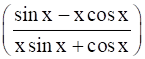
![]()
![]()
![]()
![]()
(iv) (uv)′ = u′v + uv′ (Leibnitz or product rule)
Let us take u = (![]() ) and v = (
) and v = (![]() )
)
![]()
Applying Product rule for finding the term xcosx in u’
(gh)′ = g′h + gh′
Taking g = xand h = cosx
[![]() ]’ = (1) (cosx) + x (-sinx)
]’ = (1) (cosx) + x (-sinx)
[![]() ]’ = cosx – x sinx
]’ = cosx – x sinx
Applying the above obtained value for finding u’
u’ = cosx – (cosx – x sinx)
u’ = x sinx
![]()
Applying Product rule for finding the term xsinx in v’
(gh)′ = g′h + gh′
Taking g = xand h = sinx
[![]() ]’ = (1) (sinx) + x (cosx)
]’ = (1) (sinx) + x (cosx)
[![]() ]’ = sinx + x cosx
]’ = sinx + x cosx
Applying the above obtained value for finding v’
v’ = sinx + x cosx - sinx
v’ = x cosx
Putting the above obtained values in the formula:-
![]()
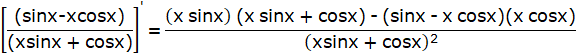
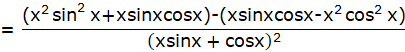
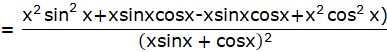
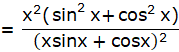
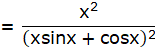
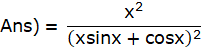
1