Find the principal solutions of each of the following equations :
(i) 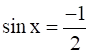
(ii) ![]()
(iii) tan x = -1
(iv) ![]()
(v) ![]()
(vi) ![]()
To Find: Principal solution.
(i) Given: 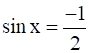
Formula used: sin![]() = sin
= sin![]() = n
= n![]() + (-1)n
+ (-1)n![]() , n
, n![]() I
I
By using above formula, we have
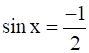 = -sin
= -sin![]() = sin(
= sin(![]() = sin
= sin![]() x = n
x = n![]() +
+![]() (-1)n
(-1)n
Put n= 0 ![]() x = 0
x = 0![]() +
+![]() (-1)0
(-1)0![]() x =
x = ![]()
Put n= 1 ![]() x = 1
x = 1![]() +
+![]() (-1)1
(-1)1![]() x =
x = ![]() 1
1 ![]() x =
x = ![]() =
= ![]()
[ NOTE: ![]() =
=![]() ]
]
So principal solution is x= ![]() and
and ![]()
(ii) Given: ![]()
![]() cosx =
cosx = ![]()
Formula used: cos![]() = cos
= cos![]() = 2n
= 2n![]() , n
, n![]() I
I
By using above formula, we have
cosx = ![]() = cos
= cos![]() x = 2n
x = 2n![]() , n
, n![]() I
I
Put n= 0 ![]() x = 2 × 0 ×
x = 2 × 0 × ![]() x =
x = ![]()
Put n= 1 ![]() x = 2
x = 2![]() x =
x = ![]() ,
,![]() x =
x = ![]() ,
,![]()
[![]() 2
2![]() So it is not include in principal solution]
So it is not include in principal solution]
So principal solution is x= ![]() and
and ![]()
(iii) Given: tan x = -1
Formula used: tan![]() = tan
= tan![]() = n
= n![]() , n
, n![]() I
I
By using above formula, we have
tan x = -1 = tan![]() x = n
x = n![]() , n
, n![]() I
I
Put n= 0 ![]() x = n
x = n![]() x =
x = ![]()
Put n= 1 ![]() x =
x = ![]() x =
x = ![]() x =
x = ![]()
So principal solution is x= ![]() and
and ![]()
(iv) Given: ![]()
![]() cosec x =
cosec x = ![]()
We know that cosec![]() sin
sin![]() = 1
= 1
So sinx = ![]()
Formula used: sin![]() = sin
= sin![]() = n
= n![]() + (-1)n
+ (-1)n![]() , n
, n![]()
By using above formula, we have
sinx = ![]() = sin
= sin![]() = n
= n![]() +
+![]() (-1)n
(-1)n
Put n= 0 ![]() x = 0
x = 0![]() +
+![]() (-1)0
(-1)0![]() x =
x = ![]()
Put n= 1 ![]() x = 1
x = 1![]() +
+![]() (-1)1
(-1)1![]() x =
x = ![]() 1
1 ![]() x =
x = ![]() =
= ![]()
[ NOTE: ![]() =
=![]() ]
]
So principal solution is x= ![]() and
and ![]()
(v) Given: tan x = -![]()
Formula used: tan![]() = tan
= tan![]() = n
= n![]() , n
, n![]() I
I
By using above formula, we have
tan x = -![]() = tan
= tan![]() x = n
x = n![]() , n
, n![]() I
I
Put n= 0 ![]() x = n
x = n![]() x =
x = ![]()
Put n= 1 ![]() x =
x = ![]() x =
x = ![]()
So principal solution is x= ![]() and
and ![]()
(vi) Given: ![]()
![]() sec x =
sec x = ![]()
We know that sec![]() cos
cos![]() = 1
= 1
So cosx = ![]()
Formula used: cos![]() = cos
= cos![]() = 2n
= 2n![]() , n
, n![]() I
I
By using the above formula, we have
cosx = ![]() = cos
= cos![]() x = 2n
x = 2n![]() , n
, n![]() I
I
Put n= 0 ![]() x = 2n
x = 2n![]() x =
x = ![]()
Put n= 1 ![]() x = 2
x = 2![]() x =
x = ![]() ,
,![]() x =
x = ![]() ,
,![]()
[![]() 2
2![]() So it is not include in principal solution]
So it is not include in principal solution]
So principal solution is x= ![]() and
and ![]()