Find the general solution of each of the following equations:

(i)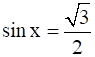


(ii) cos x = 1


(iii)


To Find: General solution.


(i) Given: sin x =


Formula used: sin = sin = n + (-1)n , n I


By using above formula, we have


sin x = = sin x = n + (-1)n .


So general solution is x = n + (-1)n . where n I


(ii) Given: cos x = 1


Formula used: cos = cos = 2n , n I


By using above formula, we have


cos x = 1= cos(0) x = 2n , n I


So general solution is x = 2n where n I


(iii) Given: sec x =


We know that sec cos = 1


So cosx =


Formula used: cos = cos = 2n , n I


By using above formula, we have


cosx = = cos x = 2n , n I


So general solution is x = 2n where n I


1