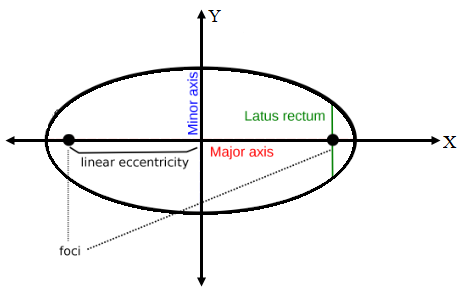
Let the equation of the required ellipse is

…(i)

It is given that,

We know that,

and Length of Minor Axis = 2b

So, according to the given condition,

⇒ 2b = a …(ii)

Now, we have to find the eccentricity

We know that,

…(iii)

where, c² = a² – b²

So, c² = (2b)² – b² [from (ii)]

⇒ c² = 4b² – b²

⇒ c² = 3b²

⇒ c = √3b²

⇒ c = b√3

Substituting the value of c and a in eq. (iii), we get