Let Q be the set of all positive rational numbers.
(i) Show that the operation * on Q + defined by 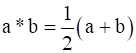 is a binary operation.
is a binary operation.
(ii) Show that * is commutative.
(iii) Show that * is not associative.
(i)Let a = 1, b = 2![]() Q +
Q +
a*b = ![]() = 1.5
= 1.5![]() Q +
Q +
* is closed and is thus a binary operation on Q +
(ii) a*b = ![]() = 1.5
= 1.5
And b*a = ![]() = 1.5
= 1.5
Hence * is commutative.
(iii)let c = 3.
(a*b)*c = 1.5*c = ![]()
a*(b*c) = a*![]() = 1*2.5 =
= 1*2.5 = ![]() = 1.75
= 1.75
hence * is not associative.
1