RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 4. Inverse Trigonometric Functions

Subject: Maths - Class 12th

Q. No. 3 B of Exercise 4C

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

3 B

Prove that:


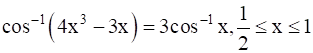
To Prove: cos-1 (4x3 – 3x) = 3 cos-1 x


Formula Used: cos 3A = 4 cos3 A – 3 cos A


Proof:


LHS = cos-1 (4x3 – 3x) … (1)


Let x = cos A … (2)


Substituting (2) in (1),


LHS = cos-1 (4 cos3 A – 3 cos A)


= cos-1 (cos 3A)


= 3A


From (2), A = cos-1 x,


3A = 3 cos-1 x


= RHS


Therefore, LHS = RHS


Hence proved.


Chapter Exercises

Exercise 4A
Exercise 4B
Exercise 4C
Exercise 4D
Objective Questions

More Exercise Questions

1 A

Prove that:
1 B

Prove that:
2

Prove that:
3 A

Prove that:
3 B

Prove that:
3 C

Prove that:
3 D

Prove that:
4 A

Prove that:
4 B

Prove that:
4 C

Prove that:
4 D

Prove that:
5 A

Prove that:
5 B

Prove that:
5 C

Prove that:
6 A

Prove that:
6 B

Prove that:
6 C

Prove that:
6 D

Prove that:
6 E

Prove that:
6 F

Prove that:
6 G

Prove that:
6 H

Prove that:
7 A

Prove that:
7 B

Prove that:
7 C

Prove that:
7 D

Prove that:
7 E

Prove that:
7 F

Prove that:
7 G

Prove that:
8 A

Solve for x:
8 B

Solve for x:
8 C

Solve for x:
8 D

Solve for x:
8 E

Solve for x:
9 A

Solve for x :
9 B

Solve for x :
9 C

Solve for x :

Students Store