RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 4. Inverse Trigonometric Functions

Subject: Maths - Class 12th

Q. No. 8 A of Exercise 4C

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

8 A

Solve for x:


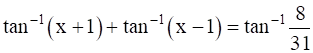
To find: value of x


Formula Used:


Given:


LHS




Therefore,


Taking tangent on both sides, we get



⇒ 62x = 16 – 8x2


⇒ 8x2 + 62x – 16 = 0


⇒ 4x2 + 31x – 8 = 0


⇒ 4x2 + 32x – x – 8 = 0


⇒ 4x × (x + 8) – 1 × (x + 8) = 0


⇒ (4x – 1) × (x + 8) = 0



Therefore, are the required values of x.


Chapter Exercises

Exercise 4A
Exercise 4B
Exercise 4C
Exercise 4D
Objective Questions

More Exercise Questions

1 A

Prove that:
1 B

Prove that:
2

Prove that:
3 A

Prove that:
3 B

Prove that:
3 C

Prove that:
3 D

Prove that:
4 A

Prove that:
4 B

Prove that:
4 C

Prove that:
4 D

Prove that:
5 A

Prove that:
5 B

Prove that:
5 C

Prove that:
6 A

Prove that:
6 B

Prove that:
6 C

Prove that:
6 D

Prove that:
6 E

Prove that:
6 F

Prove that:
6 G

Prove that:
6 H

Prove that:
7 A

Prove that:
7 B

Prove that:
7 C

Prove that:
7 D

Prove that:
7 E

Prove that:
7 F

Prove that:
7 G

Prove that:
8 A

Solve for x:
8 B

Solve for x:
8 C

Solve for x:
8 D

Solve for x:
8 E

Solve for x:
9 A

Solve for x :
9 B

Solve for x :
9 C

Solve for x :

Students Store