Express the matrix 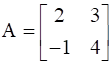 as the sum of a symmetric matrix and a skew-symmetric matrix.
as the sum of a symmetric matrix and a skew-symmetric matrix.
Given 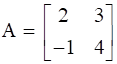 , As for a symmetric matrix A’ = A hence
, As for a symmetric matrix A’ = A hence
A + A’ = 2A
A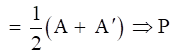 (Symmetric Matrix)
(Symmetric Matrix)
Similarly for a skew symmetric matrix since A’ = -A hence
A-A’ = 2A
A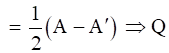 (Skew Symmetric Matrix)
(Skew Symmetric Matrix)
So a matrix can be represented as a sum of a symmetric matrix P and skew symmetric matrix Q.
First, we will find the transpose of matrix A,
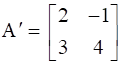
Now using the above formulas,
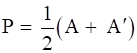
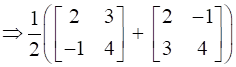
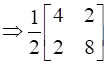
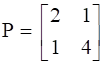
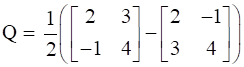
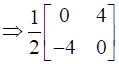
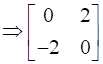
Hence A = P + Q
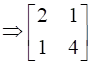 +
+ 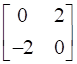 [Matrix A as the sum of P and Q]
[Matrix A as the sum of P and Q]
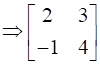
1