For the following matrices, verify that A(BC) = (AB)C :
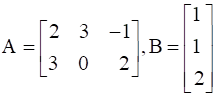and C = [1 -2]
Given :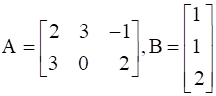 
and C = [1 -2]
Matrix A is of order 2 
3 , matrix B is of order 3 
1 and matrix C is of order 1 
2
To show : matrix A(BC) = (AB)C
Formula used :
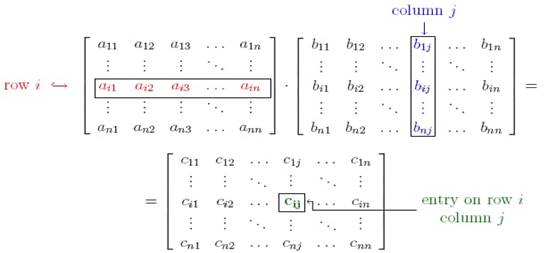
Where cij = ai1b1j + ai2b2j + ai3b3j + ……………… + ainbnj
If A is a matrix of order a 
b and B is a matrix of order c 
d ,then matrix AB exists and is of order a 
d ,if and only if b = c
If A is a matrix of order a 
b and B is a matrix of order c 
d ,then matrix BA exists and is of order c 
b ,if and only if d = a
For matrix BC, a = 3,b = c = 1,d = 2 ,thus matrix BC is of order 3 
2
Matrix BC =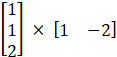 
= 
= 
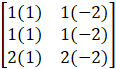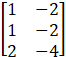
Matrix BC =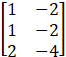 
For matrix A(BC),a = 2 ,b = c = 3 ,d = 2 ,thus matrix A(BC) is of order 2 x 2
Matrix A(BC) =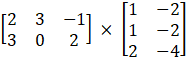 
= 
Matrix A(BC) = 
= 
Matrix A(BC) = 
Matrix A(BC) = 
For matrix AB, a = 2,b = c = 3,d = 1 ,thus matrix BC is of order 2 
1
Matrix AB =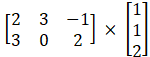
= 
Matrix AB = 
= 
Matrix AB = 
For matrix (AB)C, a = 2,b = c = 1,d = 2 ,thus matrix (AB)C is of order 2 
2
Matrix (AB)C = 
= 
= 
Matrix (AB)C = 
Matrix A(BC) = (AB)C = 