If 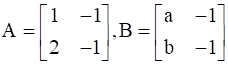 and (A + B)2 = (A2 + B2) then find the values of a and b.
and (A + B)2 = (A2 + B2) then find the values of a and b.
Given : 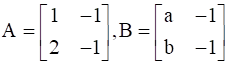
(A + B)2 = (A2 + B2)
To find : a and b
Formula used :
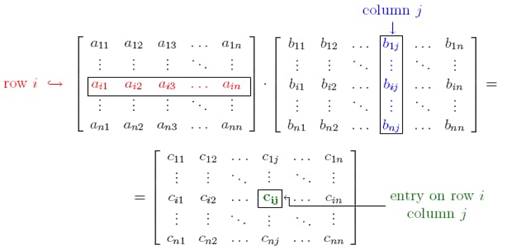
Where cij = ai1b1j + ai2b2j + ai3b3j + ……………… + ainbnj
If A is a matrix of order a ![]() b and B is a matrix of order c
b and B is a matrix of order c ![]() d ,then matrix AB exists and is of order a
d ,then matrix AB exists and is of order a ![]() d ,if and only if b = c
d ,if and only if b = c
A + B = ![]() +
+ ![]() =
= ![]() =
= ![]()
A + B = ![]()
(A + B)2 = ![]() ×
× ![]() =
= ![]()
(A + B)2 = ![]() =
= ![]()
(A + B)2 = ![]()
A2 = ![]() ×
× ![]() =
= ![]() =
= ![]()
A2 = ![]()
B2 = ![]() ×
× ![]() =
= ![]() =
= ![]()
B2 = ![]()
(A2 + B2) = ![]() +
+ ![]() =
= ![]()
(A2 + B2) = ![]()
It is given that (A + B)2 = (A2 + B2)
![]() =
= ![]()
Equating similar terms in the given matrices we get,
2 – 2a = -a + 1 and -2b = -b + 1
2 – 1 = -a + 2a and -2b + b = 1
1 = a and -b = 1
a = 1 and b = -1
1