If x ≠ y ≠ z and 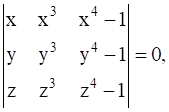 prove that xyz (xy + yz + zx) = (x + y + z).
prove that xyz (xy + yz + zx) = (x + y + z).
By properties of determinants, we can split the given determinant into 2 parts
→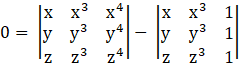
Taking x, y, z common from R1, R2, R3 respectively
→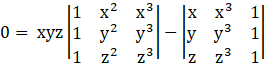
Operating R1→R1-R3, R2→R2- R3
→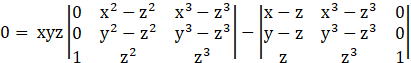
→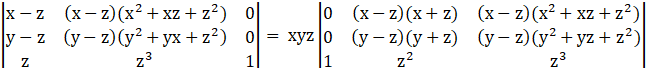
Taking (x-z) and (y-z) common from R1, R2
→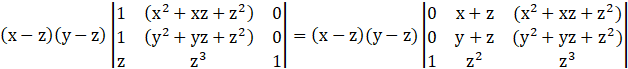
Expanding with R3
→y2+yz+z2-x2-xz-z2 = xyz(xy2+xyz+xz2+zy2+yz2+z3-x2y-xyz-yz2-x2z-xz2-z3)
→ (y-x)(y+x) +z(y-x) =xyz(xy2+zy2 -x2y -x2z)
→(y-x)(x+y+z)=xyz(xy(y-x)+z(y2-x2))
→(y-x)(x+y+z)= xyz(xy(y-x)+z(x+y)(y-x))
→(y-x)(x+y+z) = xyz(xy(y-x)+(xz+yz)(y-x))
→(y-x)(x+y+z)= xyz(y-x)(xy+xz+yz)
→x+y+z = xyz(xy+xz+yz)
Hence Proved
1