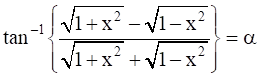Book: RD Sharma - Mathematics (Volume 1)
Chapter: 4. Inverse Trigonometric Functions
Subject: Maths - Class 12th
Q. No. 1 of MCQ
Listen NCERT Audio Books - Kitabein Ab Bolengi
Choose the correct answer
If 
, then x2 =
We are given that,
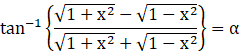
We need to find the value of x2.
Take,
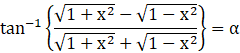
Multiply on both sides by tangent.
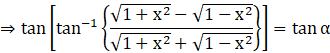
Since, we know that tan(tan-1 x) = x.
So,
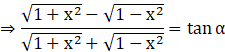
Or
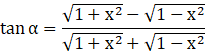
Now, we need to simplify it in order to find x2. So, rationalize the denominator by multiplying and dividing by 
.
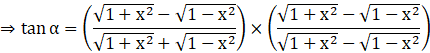
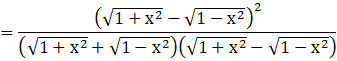
Note the denominator is in the form: (x + y)(x – y), where
(x + y)(x – y) = x2 – y2
So,
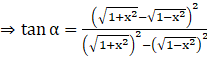…(i)
Numerator:
Applying the algebraic identity in the numerator, (x – y)2 = x2 + y2 – 2xy.
We can write as,
Again using the identity, (x + y)(x – y) = x2 – y2.
…(ii)
Denominator:
Solving the denominator, we get
…(iii)
Substituting values of Numerator and Denominator from (ii) and (iii) in equation (i),
By cross-multiplication,
⇒ x2 tan α = 1 – √(1 – x4)
⇒ √(1 – x4) = 1 – x2 tan α
Squaring on both sides,
⇒ [√(1 – x4)]2 = [1 – x2 tan α]2
⇒ 1 – x4 = (1)2 + (x2 tan α)2 – 2x2 tan α [∵, (x – y)2 = x2 + y2 – 2xy]
⇒ 1 – x4 = 1 + x4 tan2 α – 2x2 tan α
⇒ x4 tan2 α – 2x2 tan α + x4 + 1 – 1 = 0
⇒ x4 tan2 α – 2x2 tan α + x4 = 0
Rearranging,
⇒ x4 + x4 tan2 α – 2x2 tan α = 0
⇒ x4 (1 + tan2 α) – 2x2 tan α = 0
⇒ x4 (sec2 α) – 2x2 tan α = 0 [∵, sec2 x – tan2 x = 1 ⇒ 1 + tan2 x = sec2 x]
Taking x2 common from both terms,
⇒ x2 (x2 sec2 α – 2 tan α) = 0
⇒ x2 = 0 or (x2 sec2 α – 2 tan α) = 0
But x2 ≠ 0 as according to the question, we need to find some value of x2.
⇒ x2 sec2 α – 2 tan α = 0
⇒ x2 sec2 α = 2 tan α
In order to find the value of x2, shift sec2 α to Right Hand Side (RHS).
Putting 
,
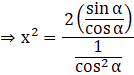
⇒ x2 = 2 sin α cos α
Using the trigonometric identity, 2 sin x cos x = sin 2x.
⇒ x2 = sin 2α
