Book: RD Sharma - Mathematics (Volume 1)
Chapter: 4. Inverse Trigonometric Functions
Subject: Maths - Class 12th
Q. No. 2 of MCQ
Listen NCERT Audio Books - Kitabein Ab Bolengi
2
Choose the correct answer
The value of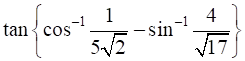 
is
We need to find the value of
Let,
Let us find sin a and cos b.
For sin a,
We know the trigonometric identity, sin2 a + cos2 a = 1
⇒ sin2 a = 1 – cos2 a
⇒ sin a = √(1 – cos2 a)
Substituting the value of cos a,
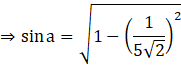
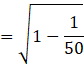
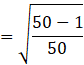
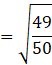
We have 
.
So, we can find tan a.
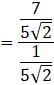
⇒ tan a = 7 …(i)
For cos b,
We know the trigonometric identity,
sin2 b + cos2 b = 1
⇒ cos2 b = 1 – sin2 b
⇒ cos b = √(1 – sin2 b)
Substituting the value of sin b,
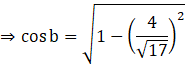
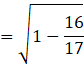
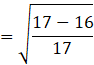
We have 
.
So, we can find tan b.
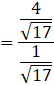
⇒ tan b = 4 …(ii)
We can write as,
Now, we need to solve Right Hand Side (RHS).
We know the trigonometric identity,
Substituting the values of tan a and tan b from (i) and (ii),
So,
1
