We need to find the value of 2 tan^-1 |cosec(tan^-1 x) – tan(cot^-1 x)|.

So, take

2 tan^-1 |cosec(tan^-1 x) – tan(cot^-1 x)|

Using property of inverse trigonometry,

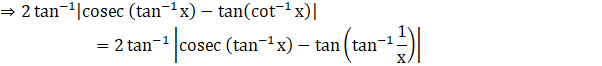
Now, let y = tan^-1 x

So, tan y = x

Substituting the value of tan^-1 x and x in the equation,

Put,

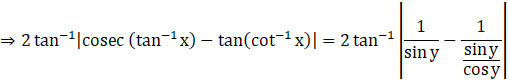
Since, we know the trigonometric identity,

1 – cos 2y = 2 sin² y

Also, sin 2y = 2 sin y cos y

We get,

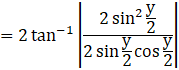
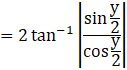
Since,

Then,

⇒ 2 tan^-1 |cosec(tan^-1 x) – tan(cot^-1 x)| = y

Put y = tan^-1 x as let above.

⇒ 2 tan^-1 |cosec(tan^-1 x) – tan(cot^-1 x)| = tan^-1 x