Book: RD Sharma - Mathematics (Volume 1)
Chapter: 4. Inverse Trigonometric Functions
Subject: Maths - Class 12th
Q. No. 5 of MCQ
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Choose the correct answer
The positive integral solution of the equation 
is
We need to find the positive integral solution of the equation:
Using property of inverse trigonometry,
Also,
Taking,
Using the property of inverse trigonometry,
Similarly,
Taking tangent on both sides of the equation,
Using property of inverse trigonometry,
tan(tan-1 A) = A
Applying this property on both sides of the equation,
Simplifying the equation,
Cross-multiplying in the equation,
⇒ xy + 1 = 3(y – x)
⇒ xy + 1 = 3y – 3x
⇒ xy + 3x = 3y – 1
⇒ x(y + 3) = 3y – 1
We need to find positive integral solutions using the above result.
That is, we need to find solution which is positive as well as in integer form. A positive integer are all natural numbers.
That is, x, y > 0.
So, keep the values of y = 1, 2, 3, 4, … and find x.
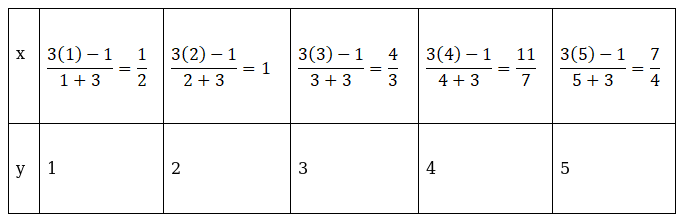
Note that, only at y = 2, value is x is positive integer.
Thus, the positive integral solution of the given equation is x = 1, y = 2.
