RD Sharma - Mathematics (Volume 1)

Book: RD Sharma - Mathematics (Volume 1)

Chapter: 4. Inverse Trigonometric Functions

Subject: Maths - Class 12th

Q. No. 8 of MCQ

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

8

Choose the correct answer

The number of solutions of the equation 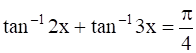is


We need to find the number of solutions of the equation,


We shall apply the property of inverse trigonometry, that is,



So,




Taking tangent on both sides of the equation,



Using property of inverse trigonometry,


tan(tan-1 A) = A


Also,



We get,



Simplifying it,


⇒ 5x = 1 – 6x2


⇒ 6x2 + 5x – 1 =0


Since, this is a quadratic equation, it is clear that it will have 2 solutions.


Let us check:


We have,


6x2 + 5x – 1 = 0


⇒ 6x2 + 6x – x – 1 = 0


⇒ 6x(x + 1) – (x + 1) = 0


⇒ (6x – 1)(x + 1) = 0


⇒ (6x – 1) = 0 or (x + 1) = 0


⇒ 6x = 1 or x = -1



Hence, there are 2 solutions of the given equation.

Chapter Exercises

Exercise 4.1
Exercise 4.2
Exercise 4.3
Exercise 4.4
Exercise 4.5
Exercise 4.6
Exercise 4.7
Exercise 4.8
Exercise 4.9
Exercise 4.10
Exercise 4.11
Exercise 4.12
Exercise 4.13
Exercise 4.14
Very short answer
MCQ

More Exercise Questions

1

Choose the correct answer

If , then x2 =
2

Choose the correct answer

The value of is
3

Choose the correct answer

is equal to
4

Choose the correct answer

If , then


5

Choose the correct answer

The positive integral solution of the equation is
6

Choose the correct answer

If , then x =
7

Choose the correct answer

is equal to
8

Choose the correct answer

The number of solutions of the equation is
9

Choose the correct answer

If and , then
10

Choose the correct answer

The number of real solutions of the equation is
11

Choose the correct answer

If x < 0, y < 0 such that xy = 1, then tan–1x + tan–1y equals
12

Choose the correct answer

If then, =
13

Choose the correct answer

If , then


14

Choose the correct answer

If , , then α – β =
15

Choose the correct answer

Let . Then f(8 π/9) =
16

Choose the correct answer

is equal to
17

Choose the correct answer

If , then 9x2 – 12xy cos θ + 4y2 is equal to
18

Choose the correct answer

If tan–1 3 + tan–1x = tan–1 8, then x =
19

Choose the correct answer

The value of is
20

Choose the correct answer

The value of is
21

Choose the correct answer

is equal to
22

Choose the correct answer

If , then one of the possible values of θ is
23

Choose the correct answer

If , then x is equal to
24

Choose the correct answer

If , then the value of x is
25

Choose the correct answer

If , then the value of x is
26

Choose the correct answer

If , then
27

Choose the correct answer

In a ΔABC, If C is a right angle, then


28

Choose the correct answer

The value of is
29

Choose the correct answer
30

Choose the correct answer

If tan–1 (cot θ) = 2 θ, then θ =
31

Choose the correct answer

If , where a, x ∈ (0, 1) then, the value of x is
32

Choose the correct answer

The value of is equal to
33

Choose the correct answer

If x > 1, then is equal to
34

Choose the correct answer

The domain of is
35

Choose the correct answer

The value of is

Students Store