Choose the correct answer
If 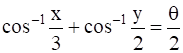 , then
, then 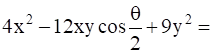
We are given with,
![]() …(i)
…(i)
We need to find the value of
![]()
Take Left Hand Side (LHS) of equation (i),
Using the property of inverse trigonometry,
![]()
Putting ![]() and
and ![]() ,
,
![]()
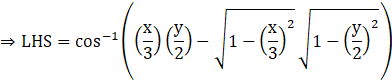
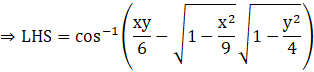
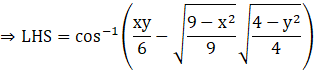
Equate LHS to RHS.
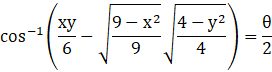
Taking cosine on both sides,
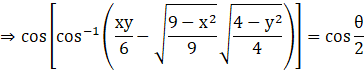
Using property of inverse trigonometry,
cos(cos-1 A) = A
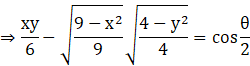
Simplifying the equation,
![]()
![]()
![]()
![]()
Squaring on both sides,
![]()
Using algebraic identity,
(A – B)2 = A2 + B2 – 2AB
![]()
![]()
![]()
![]()
Using trigonometric identity,
cos 2θ = cos2 θ – sin2 θ …(ii)
sin2 θ + cos2 θ = 1 ⇒ sin2 θ = 1 – cos2 θ …(iii)
Putting value of sin2 θ from equation (iii) in equation (ii), we get
cos 2θ = cos2 θ – (1 – cos2 θ)
Or, cos 2θ = cos2 θ – 1 + cos2 θ
Or, cos 2θ = 2 cos2 θ – 1
Or, 2 cos2 θ = cos 2θ + 1
Replace θ by θ/2.
![]()
![]()
Substituting the value of ![]() in
in
![]()
![]()
![]()
![]()
![]()
1