Book: RD Sharma - Mathematics (Volume 1)
Chapter: 4. Inverse Trigonometric Functions
Subject: Maths - Class 12th
Q. No. 25 of MCQ
Listen NCERT Audio Books - Kitabein Ab Bolengi
Choose the correct answer
If 
, then the value of x is
We are given that,
…(i)
We need to find the value of x.
Using the property of inverse trigonometry,
Replace A by 
and B by 
.
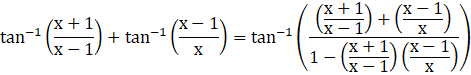
Putting this value in equation (i),
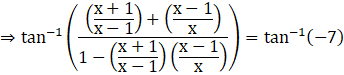
Taking tangent on both sides,
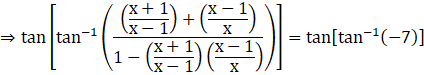
Using the property of inverse trigonometry,
tan(tan-1 A) = A
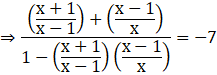
Cross-multiplying, we get
Simplifying the equation in order to find the value of x,
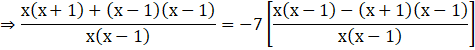
Let us cancel the denominator from both sides of the equation.
⇒ x(x + 1) + (x – 1)(x – 1) = -7[x(x – 1) – (x + 1)(x – 1)]
⇒ x2 + x + (x – 1)2 = -7[x2 – x – (x + 1)(x – 1)]
Using the algebraic identity,
(a – b) = a2 + b2 – 2ab
And, (a + b)(a – b) = a2 – b2
⇒ x2 + x + x2 + 1 – 2x = -7[x2 – x – (x2 – 1)]
⇒ 2x2 – x + 1 = -7[x2 – x – x2 + 1]
⇒ 2x2 – x + 1 = -7[1 – x]
⇒ 2x2 – x + 1 = -7 + 7x
⇒ 2x2 – x – 7x + 1 + 7 = 0
⇒ 2x2 – 8x + 8 = 0
⇒ 2(x2 – 4x + 4) = 0
⇒ x2 – 4x + 4 = 0
We need to solve the quadratic equation to find the value of x.
⇒ x2 – 2x – 2x + 4 = 0
⇒ x(x – 2) – 2(x – 2) = 0
⇒ (x – 2)(x – 2) = 0
⇒ x = 2 or x = 2
Hence, x = 2.
