Book: RD Sharma - Mathematics (Volume 1)
Chapter: 4. Inverse Trigonometric Functions
Subject: Maths - Class 12th
Q. No. 28 of MCQ
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Choose the correct answer
The value of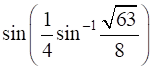 
is
We need to find the value of
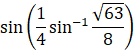
Let 
Now, take sine on both sides,
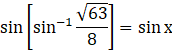
Using the property of inverse trigonometry,
sin(sin-1 A) = A
Let us find the value of cos x.
We know by trigonometric identity, that
sin2 x + cos2 x = 1
⇒ cos2 x = 1 – sin2 x
Put the value of sin x,
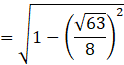
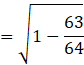
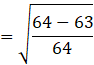
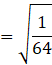
We have,
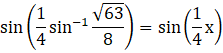
…(i)
Using the trigonometric identity,
cos 2x = cos2 x – sin2 x
⇒ cos 2x = (1 – sin2x) – sin2 x [∵, sin2 x + cos2 x = 1]
⇒ cos 2x = 1 – sin2 x – sin2 x
⇒ cos 2x = 1 – 2 sin2 x
Or,
2 sin2 x = 1 – cos 2x
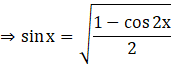
Replacing x by x/4,
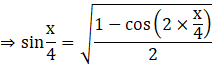
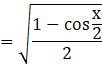
Substituting the value of 
in equation (i),
…(ii)
Using the trigonometric identity,
cos 2x = cos2 x – sin2 x
⇒ cos 2x = cos2 x – (1 – cos2 x) [∵, sin2 x + cos2 x = 1]
⇒ cos 2x = cos2 x – 1 + cos2x
⇒ cos 2x = 2 cos2 x – 1
Or,
2 cos2 x = 1 + cos 2x
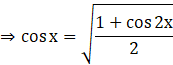
Replacing x by x/2,
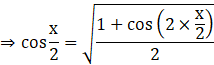
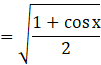
Substituting the value of 
in equation (ii),
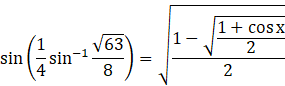
Put the value of cos x as found above, cos x = 1/8.
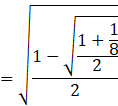
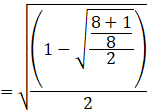
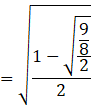
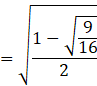
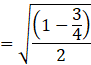
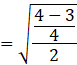
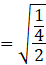
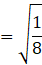
