RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 33. Binomial Distribution

Subject: Maths - Class 12th

Q. No. 10 of Very Short Answer

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

10

If for a binomial distribution P (X = 1) = P (X = 2) = α, write P (X= 4) in terms of α.

Given:


P (X = 1) = P (X = 2) = α


P (X= 4)=?


P(x=r)= nCr pr qn-r


P(x=1)= nC1 p1 qn-1


=npqn-1 (1)


P(x=2)= nC2 p2 qn-2


(2)


Equating both equations ,we have:




2q = (n-1) p


4q2 = (n-1)2 p2


P(x=4)= nC4 p4 qn-4






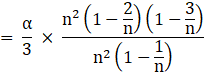
For large n; n


0


So,


Chapter Exercises

Exercise 33.2
Exercise 33.1
Very Short Answer
MCQ

More Exercise Questions

1

In a binomial distribution, if n = 20, q = 0.75, then write its mean.
2

If in a binomial distribution mean is 5 and variance is 4, write the number of trials.
3

In a group of 200 items, if the probability of getting a defective item is 0.2, write the mean of the distribution.
4

If the mean of a binomial distribution is 20 and its standard deviation is 4, find p.
5

The mean of a binomial distribution is 10 and its standard deviation is 2, write the value of q.
6

If the mean and variance of a random variable X having a binomial distribution are 4 and 2 respectively, find P (X = 1).
7

If the mean and variance of a binomial variate X are 2 and 1 respectively, find P(X > 1).
8

If in a binomial distribution n = 4 and find q.
9

If the mean and variance of a binomial distribution are 4 and 3 respectively, find the probability of no-success.
10

If for a binomial distribution P (X = 1) = P (X = 2) = α, write P (X= 4) in terms of α.
11

An unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
12

If X follows binomial distribution with parameters n = 5, p and P(X = 2) = 9 P(X = 3), then find the value of p.

Students Store