RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 33. Binomial Distribution

Subject: Maths - Class 12th

Q. No. 8 of MCQ

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

8

Mark the correct alternative in the following:

Let X denote the number of times heads occur in n tosses of a fair coin. If P (X = 4), P(X = 5) and P(X = 6) are in AP; the value of n is


Given:


P(H)=1/2=p


q=1/2


P(x=r)= nCr pr qn


P(x=4)= nC4 p4 qn-4 = nC4 pn


P(x=5)= nC5 p5 qn-5 = nC5 pn


P(x=6)= nC6 p6 qn-6 = nC6 pn


Since they are in AP;


So,


p(x=5)=


2 p(x=5) = p(x=4)+ p(x=5)


2nC5 pn = nC4 pn +nC6 pn







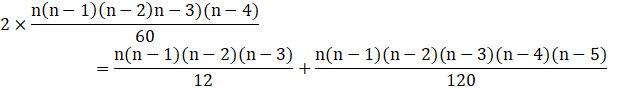
4n – 16 = 55n – 225


51n = 209


n= 4

Chapter Exercises

Exercise 33.2
Exercise 33.1
Very Short Answer
MCQ

More Exercise Questions

1

Mark the correct alternative in the following:

In a box containing 100 bulbs, 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective.
2

Mark the correct alternative in the following:

If in a binomial distribution n = 4, P(X = 0) = , then P(X = 4) equals.
3

Mark the correct alternative in the following:

A rifleman is firing at a distant target and has only 10% chance o hitting it. The least number of rounds, he must fire in order to have more than 50% chance of hitting it at least once is
4

Mark the correct alternative in the following:

A fair coin is tossed a fixed number of times. If the probability of getting seven heads is equal to that of getting nine heads, the probability of getting two heads is
5

Mark the correct alternative in the following:

A fair coin is tossed 100 times. The probability that on the tenth throw the fourth six appears is
6

Mark the correct alternative in the following:

A fair die is thrown twenty times. The probability that on the tenth throw the fourth six appears is
7

Mark the correct alternative in the following:

If X is a binomial variate with parameters n and p, where 0 < p < 1 such that is independent of n and r, then p equals.
8

Mark the correct alternative in the following:

Let X denote the number of times heads occur in n tosses of a fair coin. If P (X = 4), P(X = 5) and P(X = 6) are in AP; the value of n is
9

Mark the correct alternative in the following:

One hundred identical coins, each with probability p of showing heads are tossed once. If 0 < p < 1 and the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins, the value of p is
10

Mark the correct alternative in the following:

A fair coin is tossed 99 times. If X is the number of times heads occur, then P(X = r) is maximum when r is
11

Mark the correct alternative in the following:

The least number of times a fair coin must be tossed so that the probability of getting at least one head is at least 0.8, is
12

Mark the correct alternative in the following:

If the mean and variance of a binomial variate X are 2 and 1 respectively, then the probability that X takes a value greater than 1 is
13

Mark the correct alternative in the following:

A biased coin with probability p, 0 < p < 1, of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 2/5, then p equals.
14

Mark the correct alternative in the following:

If X follows a binomial distribution with parameters n = 8 and p = 1/2, then P (|X – 4)| ≤ 2) equals.
15

Mark the correct alternative in the following:

If X follows a binomial distribution with parameters n = 100 and p = 1/3, then P (X = r) is
16

Mark the correct alternative in the following:

A fair die is tossed eight times. The probability that a third six is observed in the eight throw is
17

Mark the correct alternative in the following:

Fifteen coupons are numbered 1 to 15. Seven coupons are selected at random, one at a time with replacement. The probability that the largest umber appearing on a selected coupon is 9, is
18

Mark the correct alternative in the following:

A five-digit number is written down at random. The probability that the number is divisible by 5 and no two consecutive digits are identical, is
19

Mark the correct alternative in the following:

A coin is tossed 10 times. The probability of getting exactly six heads is
20

Mark the correct alternative in the following:

The mean and variance of a binomial distribution are 4 and 3 respectively, then the probability of getting exactly six successes in this distribution, is
21

Mark the correct alternative in the following:

In a binomial distribution, the probability of getting success is 1/4 and standard deviation is 3. Then, its means is
22

Mark the correct alternative in the following:

A coin is tossed 4 times. The probability that at least one head turns up, is
23

Mark the correct alternative in the following:

For a binomial variate X, if n = 3 and P (X = 1) = 8 P(X = 3), then p =
24

Mark the correct alternative in the following:

A coin is tossed n times. The probability of getting at least once is greater than 0.8. Then, the least value of n, is
25

Mark the correct alternative in the following:

The probability of selecting a male or a female is same. If the probability that in an office of n persons (n – 1) males being selected is , the value of n is
26

Mark the correct alternative in the following:

A box contains 100 pens of which 10 are defective. What is the probability that out of a sample of 5 pens drawn one by one with replacement at most one is defective?
27

Mark the correct alternative in the following:

Suppose a random variable X follows the binomial distribution with parameters n and p, where 0 < p < 1. If is independent of n and r, then p equals.
28

Mark the correct alternative in the following:

The probability that is person is not a swimmer is 0.3. The probability that out of 5 persons 4 are swimmers is
29

Mark the correct alternative in the following:

Which one is not a requirement of a binomial distribution?
30

Mark the correct alternative in the following:

The probability of guessing correctly at least 8 out of 10 answers of a true false type examination is

Students Store