Mark the correct alternative in the following:
Suppose a random variable X follows the binomial distribution with parameters n and p, where 0 < p < 1. If 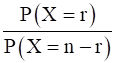 is independent of n and r, then p equals.
is independent of n and r, then p equals.
Given:
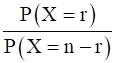
P=?
P(x=r)= nCr pr qn-r
= ![]()
P(x=n-r)= nCn-r pn-r qn-(n-r)
= nCr pn-r qr
=![]()
Put values in equation, we have:
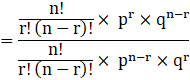
![]()
![]()
![]()
1-p=p
1=2p
P=1/2
1