The plane contains the line and the point

As, the plane contains the line,

so, the plane contains the point also.

On putting λ=1, we get another point on the plane which is i.e.

So, we got three points on the plane, they are, , and

Let,

and

So, and

Now, the normal of these two vectors i.e. and is,

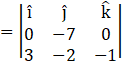
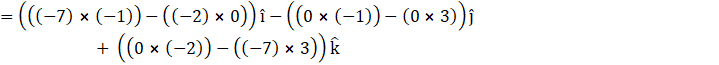
The general equation of plane is,

7(x - 1) + 21(z - 3)=0

7x - 7 + 21z - 63=0

7x + 21z=70

x + 3z=10

or,

Hence, the vector equation of the plane containing the line and the point is .