The two planes are, and

The line of intersection of planes and

is parallel to

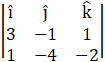
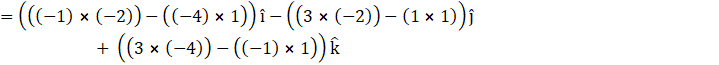
The line of intersection of planes and

is parallel to

Alternative:

The two planes are, and

or, 3x - y + z=1 and x - 4y - 2z=2

Putting, z=k, we get,

3x - y + k=1 ………………………. (1)

and x - 4y - 2k=2 …………………… (2)

Multiplying equation (2) by 3 and then subtracting equation (1) from it, we get,

3(x - 4y - 2k) - (3x - y + k)=(3×2) - 1

3x - 12y - 6k - 3x + y - k=6 - 1

- 11y - 7k=5

Substituting y, in equation (1) we get,

33x + 5 + 7k + 11k=11

18k=11 - 5 - 33x

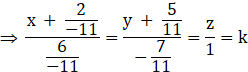
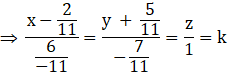
Equation of the line of intersection,

The line of intersection of planes and

is parallel to .