Mark the correct alternative in the following: If a plane passes through the point (1, 1, 1) and is perpendicular to the line 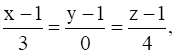then its perpendicular distance from the origin is

Question

Philoid · Accepted Answer

Let, the equation of the plane be, Ax + By + Cz + D=0, as the plane is perpendicular to, so, we have,

A=3, B=0 and C=4

As the plane passes through (1, 1, 1) we have, (A×1) + (B×1) + (C×1) + D=0

A + B + C + D=0

3 + 0 + 4 + D=0

D= - 7

So, the equation of the plane becomes, 3x + 4z - 7=0

Now, the perpendicular distance of the plane from the origin is

Hence, the perpendicular distance from the origin to the plane is units.

Mark the correct alternative in the following:If a plane passes through the point (1, 1, 1) and is perpendicular to the line then its perpendicular distance from the origin is

Mark the correct alternative in the following:
If a plane passes through the point (1, 1, 1) and is perpendicular to the line then its perpendicular distance from the origin is