Let, the point of intersection of the line

and the plane

be (x₀, y₀, z₀).

As (x₀, y₀, z₀) is the point of intersection of the line and the plane, so the position vector of this point i.e.

must satisfy both of the equation of

line and the equation of plane.

Substituting, in place of in both the equations, we

get,

And, ………………. (2)

i.e.
x₀ =2 + 3λ

y₀ = - 1 + 4λ

z₀ =2 + 12λ

Substituting, these values in equation (2) we get,

((2 + 3λ)×1) - (1×( - 1 + 4λ)) + (1×(2 + 12λ))=5

2 + 3λ + 1 - 4λ + 2 + 12λ=5

11λ=0

λ=0

∴x₀ =2 + 3λ

=2

y_0= - 1 + 4λ

= - 1

z_0=2 + 12λ

=2

Hence, the point of intersection is, (2, - 2, 2).

Now, the distance between the point ( - 1, - 5, - 10) and (2, - 1, 2) is,

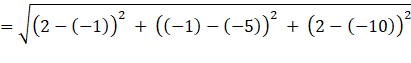
=13

Hence, the required distance between the point ( - 1, - 5, - 10) the point where the line the plane , is 13 units.