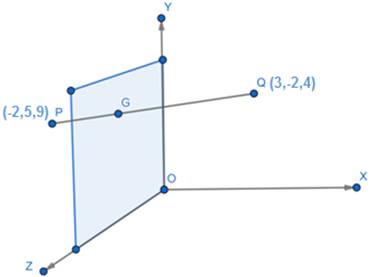
Write the ratio in which YZ-plane divides the segment joining P(–2, 5, 9) and Q(3, –2, 4).
Given the points P(-2,5,9) and Q(3,-2,4)
Let the plane YZ-plane divide line segment PQ at point G(0,y,z) in the ratio m:n.
The coordinates of the point G which divides the line joining points A(x1,y1,z1) and B(x2,y2,z2) in the ratio m:n is given by
![]()
Here, we have m:n
x1 = -2 y1 = 5 z1 = 9
x2 = 3 y2 = -2 z2 = 4
By using the above formula, we get,
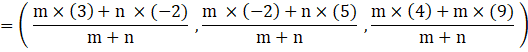
![]()
Now, this is the same point as G(0,y,z),
As the x-coordinate is zero,
![]()
[Cross Multiplying]
3m – 2n = 0 × (m + n)
3m – 2n = 0
3m = 2n
![]()
Therefore, the ratio in which the plane-YZ divides the line joining A & B is 2:3
1