If matrix 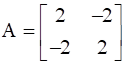 and A2 = pA, then write the value of p.
and A2 = pA, then write the value of p.
We are given that,
![]()
A2 = pA
We need to find the value of p.
First, let us find A2.
We know that, A2 = A.A
![]()
In multiplication of matrices A and A, such that A2 = Z(say):
![]()
For the calculation of z11: Dot multiply the 1st row of first matrix and the 1st column of second matrix and then sum up.
(2 -2)(2 -2) = 2 × 2 + (-2) × (-2)
⇒ (2 -2)(2 -2) = 4 + 4
⇒ (2 -2)(2 -2) = 8
So,
![]()
For the calculation of z12: Dot multiply the 1st row of first matrix and the 2nd column of second matrix and then sum up.
(2 -2)(-2 2) = 2 × -2 + (-2) × 2
⇒ (2 -2)(-2 2) = -4 – 4
⇒ (2 -2)(-2 2) = -8
So,
![]()
Similarly,
![]()
![]()
![]()
So,
![]() …(i)
…(i)
Now, let us find pA.
Multiply p by matrix A,
![]()
![]()
![]() …(ii)
…(ii)
Substituting value of A2 and pA from (i) and (ii) in
A2 = pA
![]()
We know by the property of matrices,
![]()
This implies,
a11 = b11, a12 = b12, a21 = b21 and a22 = b22
So,
2p = 8
-2p = -8
-2p = -8
2p = 8
Take equation,
2p = 8
![]()
⇒ p = 4
Thus, the value of p = 4.