We are given that,

is symmetric matrix.

We need to find the values of a and b.

We must understand what symmetric matrix is.

A symmetric matrix is a square matrix that is equal to its transpose.

A symmetric matrix ⬄ A = A^T

This means, we need to find the transpose of matrix A.

Let us take transpose of the matrix A.

We know that, the transpose of a matrix is a new matrix whose rows are the columns of the original.

We have,

1^st row of matrix A = (0 2b -2)

2^nd row of matrix A = (3 1 3)

3^rd row of matrix A = (3a 3 -1)

For matrix A^T, it will become

1^st column of A^T = 1^st row of A = (0 2b -2)

2^nd column of A^T = 2^nd row of A = (3 1 3)

3^rd column of A^T = 3^rd row of A = (3a 3 -1)

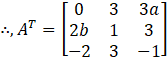
Now, as A = A^T.

Substituting the matrices A and A^T, we get

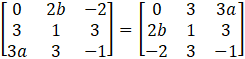
We know by the property of matrices,

This implies,

a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ and a₂₂ = b₂₂

Applying this property, we can write

2b = 3 …(i)

-2 = 3a …(ii)

3 = 2b

3a = -2

We can find a and b from equations (i) and (ii).

From equation (i),

2b = 3

From equation (ii),

-2 = 3a

Thus, we get and .