If 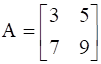 is written as A = P + Q, where as A = P + Q, where P is symmetric and Q is skew-symmetric matrix, then write the matrix P.
is written as A = P + Q, where as A = P + Q, where P is symmetric and Q is skew-symmetric matrix, then write the matrix P.
We are given that,
![]()
Where,
P = symmetric matrix
Q = skew-symmetric matrix
We need to find P.
A symmetric matrix is a square matrix that is equal to its transpose.
A symmetric matrix ⬄ P = PT
Now, let us understand what skew-symmetric matrix is.
A skew-symmetric matrix is a square matrix whose transpose equals its negative, that, it satisfies the condition
A skew symmetric matrix ⬄ QT = -Q
So, let the matrix P be
![]()
Let us calculate AT.
We know that the transpose of a matrix is a new matrix whose rows are the columns of the original.
We have,
![]()
Here,
1st row of A = (3 5)
2nd row of A = (7 9)
Transpose of this matrix A, AT will be given as
1st column of AT = 1st row of A = (3 5)
2nd column of AT = 2nd row of A = (7 9)
Then,
![]()
Substituting the matrix A and AT in P,
![]()
![]()
![]()
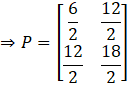
![]()
Taking transpose of P,
1st row of P = (3 6)
2nd row of P = (6 9)
Transpose of this matrix P, PT will be given as
1st column of PT = 1st row of P = (3 6)
2nd column of PT = 2nd row of P = (6 9)
Then,
![]()
Since, P = PT. Thus, P is symmetric.
Now, let the matrix Q be
![]()
Substituting the matrix A and AT in Q,
![]()
![]()
![]()
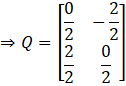
![]()
Multiplying -1 on both sides,
![]()
![]()
![]()
Taking transpose of Q,
1st row of Q = (0 -1)
2nd row of Q = (1 0)
Transpose of this matrix Q, QT will be given as
1st column of QT = 1st row of Q = (0 -1)
2nd column of QT = 2nd row of Q = (1 0)
Then,
![]()
Since, QT = -Q. Thus, Q is skew-symmetric.
Check:
![]()
Put the value of matrices P and Q.
![]()
![]()
![]()
Matrices P and Q satisfies the equation.
Hence, ![]() .
.