Mark the correct alternative in the following: For the function 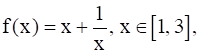the value of c for the Lagrange’s mean value theorem is

Question

Philoid · Accepted Answer

It shows that f(x) is continuous on 1, 3 and derivable on 1, 3.

So, both the conditions of Lagrange’s Theorem are satisfied.

Consequently, there exists c Є 1, 3 such that

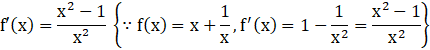
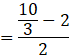
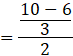
Hence, Є (1, 3) such that .

Hence, Option (B) is the answer.