Mark the correct alternative in the following: If f(x) = e x sinx in [0, π], then c in Rolle’s theorem is

Question

Philoid · Accepted Answer

As, f(x) = e^x Sin x

Differentiating the function with respect to ‘x’,

f’(x) = e^x Cos x + Sin x e^x

f’(c) = e^c Cos c + Sin c e^c

As, e^x Cos x is continuous and derivable in R.

it is contionous on and derivable on .

f(0) = e⁰ Sin (0)

= 0

f’(c) = 0

e^c Cos c + Sin c e^c = 0

e^c (Cos c + Sin c) = 0

Cos c + Sin c = 0 -------- (i)

Cos c = - Sin c

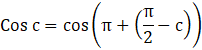
c = Є (0, )

Hence, Option (D) is the answer.