Formula:- (i) ax²+bx+c>0 for all x a>0 and b²-4ac<0

(ii) ax²+bx+c<0 for all x a<0 and b²-4ac<0

(iii) The necessary and sufficient condition for differentiable function defined on (a,b) to be strictly increasing on (a,b) is that f’(x)>0 for all x(a,b)

Given:-

f(x) = 2tanx+(2a+1)log_e |sec x|+(a – 2)x

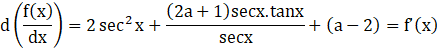
f^’(x)=2sec²x+ (2a+1) tanx + (a-2)

f^’(x)=2(tan²+1) + (2a+1).tanx +(a-2)

f^’(x)=2tan²x+2atanx+tanx+a

For increasing function

f’(x)>0

2tan²x+2atanx+tanx+ a>0

From formula (i)

(2a+1)²-8a<0