Book: RD Sharma - Mathematics (Volume 2)
Chapter: 21. Areas of Bounded Regions
Subject: Maths - Class 12th
Q. No. 2 of MCQ
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
2
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
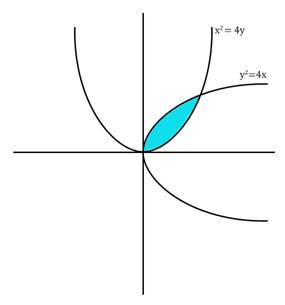
The blue area is what we need to compute. To do that we need the bounds, i.e., where the area starts and where it ends. At the points of intersection, both the equations are satisfied.
This means that at points of intersection
y2 = 4x
(from the other equation)
Let us solve this.
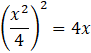
x4 = 64x
⇒ x(x3 – 64) = 0
⇒ x = 0 or x3 = 64, i.e, x = 4
So the points of intersection are (0,0) and (4,4)
Now, let’s compute the area.
If we integrate w.r.t x, we’ll have to integrate the space between the two curves from x = 0 to x =4.
i.e.,
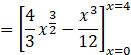
(Ans)
