x² + y² – 6x – 4y + 12 ≤ 0 can be written as –

x² – 6x + 9 – 9 +y² – 4y + 4 – 4 + 12 ≤ 0

i.e., (x - 3)² + (y – 2)² ≤ 1

So, this indicates the area enclosed by a circle centred at (3,2) with radius 1.

Now, the area of the region formed by x² + y² – 6x – 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is

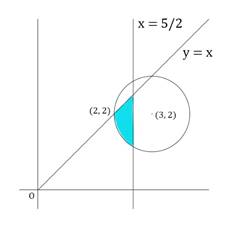
So, our bounds are x = 2 to x = 2.5

The equation for the ordinate of point on the circle from x = 2 to x = 2.5 –

(x – 3)² + (y – 2)² = 1

(y – 2)² = 1 – (x – 3)²

y – 2 = y = 2

Since we are considering the lower value of y in x = 2 to x = 2.5 (the one in y ≤ x),

y = 2 -

So, the area is –

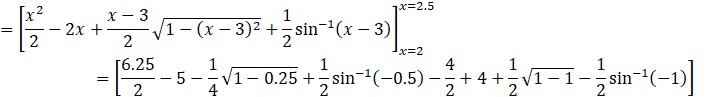
(Ans)