The question describes something like –

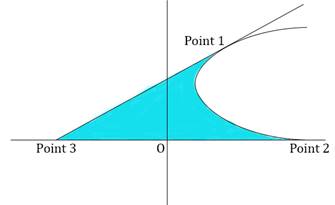
To solve the problem, we need to find the points 1, 2, and 3 first. They are the key to setting up the bounds of our integration and understanding what function to integrate.

For point 1:-

We know it is a point on the parabola with ordinate 3, at which the tangent to the parabola is taken.

Plugging in y = 3 into the equation for the parabola (y – 2)² = x – 1,

(3 – 2)² = x – 1

⇒ 1 = x – 1

⇒ x = 2

So, Point 1 is (2, 3)

For point 2:-

We need to find the point of intersection of the parabola and the x – axis.

We know that ordinate at this point is 0.

Plugging in y = 0 into the equation for the parabola (y – 2)² = x – 1,

(0 – 2)² = x – 1

⇒ 4 = x – 1

⇒ x = 5

So, Point 2 is (5, 0)

For point 3:-

Tangent at any point (x₁, y₁) for a curve is –

y – y₁ = (x – x₁)

For parabola (y – 2)² = x – 1, differentiating both sides of the equation –

2(y – 2) = 1

⇒

So, slope at point 1, i.e., (2, 3) is –

So, equation of tangent at (2, 3) is –

y – 3 = � (x – 2)

⇒ 2y – 6 = x – 2

⇒ x – 2y + 4 = 0

The tangent intersects the x – axis at point 3. At this point, ordinate is 0.

So, plugging y = 0 in the equation of the tangent x – 2y + 4 = 0, -

x – 2 �0 + 4 = 0

⇒ x = -4

So, point 3 is (-4, 0).

Now, that we have the 3 points, let’s figure out how to compute the area required.

The area we need can be divided into 3 sections –

i. x = -4 to x = 1

Here, area required = area enclosed by the tangent and the x – axis

ii. x = 1 to x = 2

Here, area required = (area enclosed by the tangent and the x – axis) – (area enclosed within the parabola)

iii. x = 2 to x = 5

Here, area required = area enclosed by the parabola and the x – axis

The parabola is (y – 2)² = x – 1

Solving for y,

y = 2 ± √(x – 1)

So, area A we need is –

(Ans)