RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 21. Areas of Bounded Regions

Subject: Maths - Class 12th

Q. No. 11 of MCQ

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

11

The area bounded by the parabola y2 = 4ax and x2 = 4ay is

This problem is the generalized form of question 2.


Let’s proceed to solve it similarly –


We need the bounds, i.e., where the area starts and where it ends. At the points of intersection, both the equations are satisfied.


This means that at points of intersection


y2 = 4ax


(from the other equation)


Let us solve this.



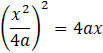
x4 = 64a3x


⇒ x(x3 – 64a3) = 0


⇒ x = 0 or x3 = 64a3, i.e, x = 4a


So the points of intersection are (0,0) and (4a,4a)


Now, let’s compute the area.


If we integrate w.r.t x, we’ll have to integrate the space between the two curves from x = 0 to x =4a.


i.e.,






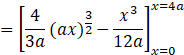
(Ans)

Chapter Exercises

Exercise 21.2
Exercise 21.3
Exercise 21.4
Exercise 21.1
MCQ

More Exercise Questions

1

If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is then the value of k is
2

The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
3

The area bounded by the curve y = loge x and x-axis and the straight line x = e is
4

The area bounded by y = 2 – x2 and x + y = 0 is
5

The area bounded by the parabola x = 4 – y2 and y-axis, in square units, is
6

If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
7

The area of the region formed by x2 + y2 – 6x – 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is
8

The area enclosed between the curves y =loge (x + e), x = logeand the x-axis is
1

The area of the region bounded by the parabola (y – 2)2 =x – 1, the tangent to it at the point with the ordinate 3 and the x-axis is
10

The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is
11

The area bounded by the parabola y2 = 4ax and x2 = 4ay is
12

The area bounded by the curve y = x4 – 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is
13

The area bounded by the parabola y2 = 4ax, latus rectum and x-axis is
14

The area of the region is
15

The area common to the parabola y = 2x2 and y = x2 + 4 is
16

The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
17

The ratio of the areas between the curves y = cosx and y = cos 2x and x-axis from x = 0 to x = π/3 is
18

The area between x-axis and curve y = cos x when 0 ≤ x ≤ 2π is
19

Area bounded by parabola y2 = x and straight line 2y = x is
20

The area bounded by the curve y = 4x – x2 and the x-axis is
21

Area enclosed between the curve y2 (2a – x) = x3 and the line x = 2a above x-axis is
22

The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
23

The area bounded by the curve y = f(x), x-axis, and the ordinates x = 1 and x = b is (b – 1) sin (3b + 4). Then, f (x) is
24

The area bounded by the curve y2 = 8x and x2 = 8y is
25

The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is
26

Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is
27

The area bounded by the curve y = x |x| and the ordinates x = –1 and x = 1 is given by
28

The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ π/2 is
29

The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
30

Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
31

Area lying between the curves y2 = 4x and y = 2x is
32

Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
33

Area of the region bounded by the cure y2 = 4x, y-axis and the line y = 3, is

Students Store