The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ π/2 is

Question

Philoid · Accepted Answer

The area we want is –

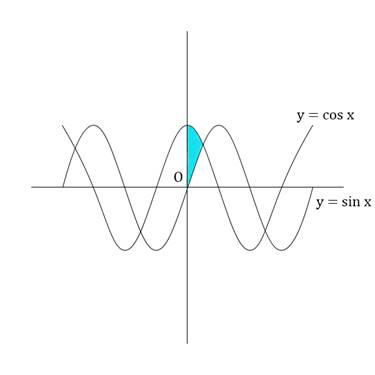
We’ll integrate w.r.t y, since area is enclosed by curves and y – axis.

Intersection point is at x = π/4, i.e., y = 1/√2

So, area A enclosed is –

A =

Using Integration by parts –

A =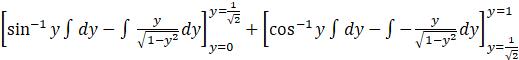

Putting u = 1 – y²

We get du = -2y dy

A =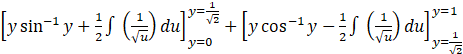

=

= π/4√2 + 1/√2 – 0 – 1 + 0 – 0 - π/4√2 + 1/√2

= √2 - 1 (Ans)