The area of the circle x 2 + y 2 = 16 enterior to the parabola y 2 = 6x is

RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 21. Areas of Bounded Regions

Subject: Maths - Class 12^th

Q. No. 29 of MCQ

Listen NCERT Audio Books - Kitabein Ab Bolengi

29

The area of the circle x² + y² = 16 enterior to the parabola y² = 6x is

The area we want is –

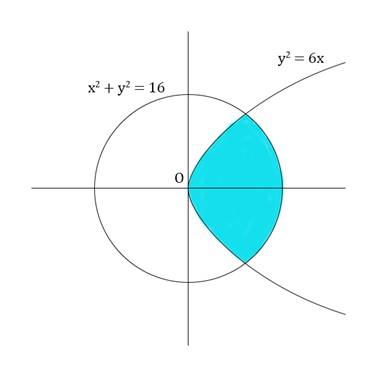
At intersection points, y² = 6x = 16 – x²

Or, x² + 6x – 16 = 0

i.e., (x + 8)(x – 2) = 0

i.e., x = -8, 2

Now x = -8 ⇒ y² = 16 – (-8)² = 16 – 64 = -48 < 0, which is not possible for y ∈ ℝ

So, x = 2

and y² = 16 – 2²

= 16 – 4

= 12

Or, y = √12 = ± 2√3

So, our bounds are y = -2√3 to y = 2√3

The area A enclosed is –

A =

Since both the functions are symmetrical about the x – axis,

A =

=

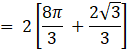
(Ans)

1

Chapter Exercises

Exercise 21.2

Exercise 21.3

Exercise 21.4

Exercise 21.1

MCQ

1

If the area above the x-axis, bounded by the curves y = 2^kx and x = 0, and x = 2 is then the value of k is

2

The area included between the parabolas y² = 4x and x² = 4y is (in square units)

3

The area bounded by the curve y = log_e x and x-axis and the straight line x = e is

4

The area bounded by y = 2 – x² and x + y = 0 is

5

The area bounded by the parabola x = 4 – y² and y-axis, in square units, is

6

If A_n be the area bounded by the curve y = (tan x)ⁿ and the lines x = 0, y = 0 and x = π/4, then for x > 2

7

The area of the region formed by x² + y² – 6x – 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is

8

The area enclosed between the curves y =log_e (x + e), x = log_eand the x-axis is

1

The area of the region bounded by the parabola (y – 2)² =x – 1, the tangent to it at the point with the ordinate 3 and the x-axis is

10

The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is

11

The area bounded by the parabola y² = 4ax and x² = 4ay is

12

The area bounded by the curve y = x⁴ – 2x³ + x² + 3 with x-axis and ordinates corresponding to the minima of y is

13

The area bounded by the parabola y² = 4ax, latus rectum and x-axis is

14

The area of the region is

15

The area common to the parabola y = 2x² and y = x² + 4 is

16

The area of the region bounded by the parabola y = x² + 1 and the straight line x + y = 3 is given by

17

The ratio of the areas between the curves y = cosx and y = cos 2x and x-axis from x = 0 to x = π/3 is

18

The area between x-axis and curve y = cos x when 0 ≤ x ≤ 2π is

19

Area bounded by parabola y² = x and straight line 2y = x is

20

The area bounded by the curve y = 4x – x² and the x-axis is

21

Area enclosed between the curve y² (2a – x) = x³ and the line x = 2a above x-axis is

22

The area of the region (in square units) bounded by the curve x² = 4y, line x = 2 and x-axis is

23

The area bounded by the curve y = f(x), x-axis, and the ordinates x = 1 and x = b is (b – 1) sin (3b + 4). Then, f (x) is

24

The area bounded by the curve y² = 8x and x² = 8y is

25

The area bounded by the parabola y² = 8x, the x-axis and the latusrectum is

26

Area bounded by the curve y = x³, the x-axis and the ordinates x = –2 and x = 1 is

27

The area bounded by the curve y = x |x| and the ordinates x = –1 and x = 1 is given by

28

The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ π/2 is

29

The area of the circle x² + y² = 16 enterior to the parabola y² = 6x is

30

Smaller area enclosed by the circle x² + y² = 4 and the line x + y = 2 is

31

Area lying between the curves y² = 4x and y = 2x is

32

Area lying in first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2, is

33

Area of the region bounded by the cure y² = 4x, y-axis and the line y = 3, is