P(A) = 0.3 , P(A∪B) = 0.5 → (Given)

Since, A and B are two independent events,

P(A∩B) = P(A) P(B)

P(A∩B) = 0.3 P(B) → (1)

Also, according to the addition theorem of probability,

P(A⋃B) = P(A) + P(B) – P(A⋂B)

0.5 = 0.3 + P(B) – 0.3P(B) → From (Given) & (1)

0.7P(B) = 0.2

P(B) = = → (2)

Putting value of P(B) in equation (1) we get,

P(A∩B) = 0.3 =

P(A∩B) = → (3)

Now,

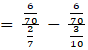→ From (3) & (2) and (Given)