Find the domain and range of the real function, defined by 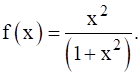Show that f is many - one.

Question

Philoid · Accepted Answer

For domain (1 + x²)≠0

⇒x²≠ - 1

⇒dom(f) = R

For the range of x:

⇒

y_min = 0 (when x = 0)

y_max = 1 (when x = ∞)

∴range of f(x) = [0,1)

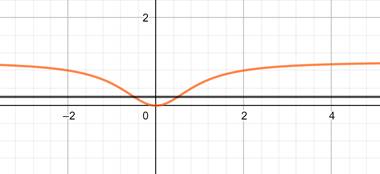
For many one the lines cut the curve in 2 equal valued points of y therefore the function f(x) is many - one.

Ans:

dom(f) = R

range(f) = [0,1)

function f(x) is many - one.