If A = 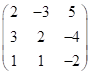 , find A - 1.
, find A - 1.
Using A - 1, solve the following system of equations:
2x – 3y + 5z = 11;
3x + 2y – 4z = - 5;
x + y – 2z = - 3.
Given,
A = 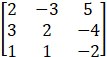
A - 1 = ![]()
The determinant of matrix A is
|A| = 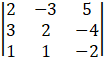
= 2( 2 × - 2 – ( - 4)×1) + 3(3× - 2 – ( - 4)×1) + 5(3×1 – 2×1)
= 2( - 4 + 4 ) + 3( - 6 + 4 ) + 5( 3 – 2 )
= 2(0) + 3( - 2) + 5(1)
= - 6 + 5
= - 1
|A| ≠ 0
∴ A - 1 is possible.
AT = 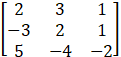
Adj(A) = 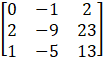
A - 1 = ![]()
A - 1 = 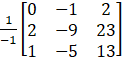
A - 1 = 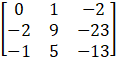
Given set of lines are : -
2x – 3y + 5z = 11
3x + 2y – 4z = - 5
x + y – 2z = - 3
Converting following equations in matrix form,
AX = B
Where A = 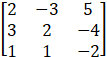 , X =
, X = 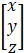 , B =
, B = 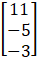
Pre - multiplying by A - 1
A - 1AX = A - 1B
IX = A - 1B
X = A - 1B
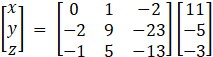
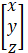 =
= 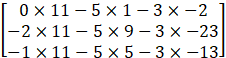
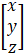 =
= 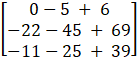
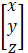 =
= 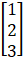
∴ x = 1 , y = 2 , z = 3
1