Prove that
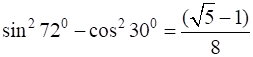
To Prove: ![]()
Taking LHS,
= sin272° - cos230°
= sin2(90° - 18°) - cos230°
= cos2 18° - cos230° …(i)
Here, we don’t know the value of cos 18°. So, we have to find the value of cos 18°
Let x = 18°
so, 5x = 90°
Now, we can write
2x + 3x = 90°
so 2x = 90° - 3x
Now taking sin both the sides, we get
sin2x = sin(90° - 3x)
sin2x = cos3x [as we know, sin(90°- 3x) = Cos3x ]
We know that,
sin2x = 2sinxcosx
Cos3x = 4cos3x - 3cosx
2sinxcosx = 4cos3x - 3cosx
⇒ 2sinxcosx - 4cos3x + 3cosx = 0
⇒ cosx (2sinx - 4cos2x + 3) = 0
Now dividing both side by cosx we get,
2sinx - 4cos2x + 3 = 0
We know that,
cos2x + sin2x = 1
or cos2x = 1 – sin2x
⇒ 2sinx – 4(1 – sin2x) + 3 = 0
⇒ 2sinx – 4 + 4sin2x + 3 = 0
⇒ 2sinx + 4sin2x – 1 = 0
We can write it as,
4sin2x + 2sinx - 1 = 0
Now applying formula
Here, ax2 + bx + c = 0
So, 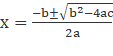
now applying it in the equation
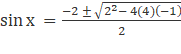
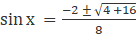
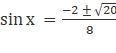
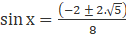
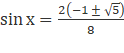
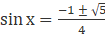
![]()
Now sin 18° is positive, as 18° lies in first quadrant.
![]()
Now, we know that
cos2x + sin2x = 1
or cosx = √1 – sin2x
∴cos 18° = √1 –sin2 18°
![]()
![]()
⇒![]()
⇒![]()
Putting the value in eq. (i), we get
= cos2 18° - cos230°
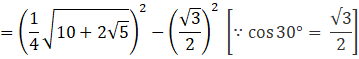
![]()
![]()
![]()
![]()
![]()
= RHS
∴ LHS = RHS
Hence Proved