To Find :

Now, let x + 2 be written as (2x + 1) + and split

Therefore ,

=

=

Now solving,

Let = u dx =

Thus, becomes

Now , = = ) =

=

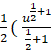Now solving ,

Now, can be written as

i.e,

Here , let x + = y dx = dy

Therefore, can be written as

Formula Used: = log |x +|+ C

Since is of the form with change in variable.

= log |y +|+ C

= log |y +|+ C

Since , x + = y and dx = dy

= log |(x + ) +|+C

Therefore,

= log |x + +|+C

Hence ,

= + log |(x + )+|+C

Therefore , = + log |(x + )+|+C