Given :

Let A, B, C & D be four points with position vectors .

Therefore,

To Prove : Points A, B, C & D are coplanar.

Formulae :

1) Vectors :

If A & B are two points with position vectors ,

Where,

then vector is given by,

2) Scalar Triple Product:

If

Then,

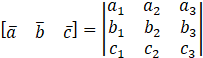
3) Determinant :

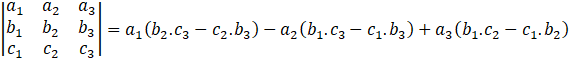
Answer :

For given position vectors,

Vectors are given by,

………eq(1)

………eq(2)

………eq(3)

Now, for vectors

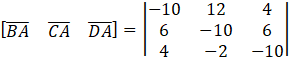
= -10(112) – 12(-84) + 4(28)

= -1120 + 1008 + 112

= 0

Hence, vectors are coplanar.

Therefore, points A, B, C & D are coplanar.

Note : Four points A, B, C & D are coplanar if and only if