When three coins are tossed simultaneously, the total number of outcomes = 2³ = 8, and the sample space is given by S= {(H,H,H),(H,H,T),(H,T,T),(H,T,H),(T,H,T),(T,T,H),(T,H,H),(T,T,T)}

Let P(A) be the probability of getting 3 heads.

The sample space of A = {(H,H,H)}

Let P(B) be the probability of getting at least head.

Probability of one head = 1 – probability of no heads = 1-1/8 = 7/8

The probability that the throw is either all heads or at least one head i.e.

Now,

Tip – By conditional probability, where is the probability of occurrence of the event A given that B has already occurred.

The probability that all coins show heads if at least one of the coins

showed a head:
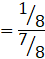