Equation of plane through the line of intersection of planes in Cartesian form is

(1)

For the standard equation of planes,

So, putting in equation (1), we have

x-3y + z + 6 + λ(x + 2y + 3z + 5)=0

(1 + λ)x + (-3 + 2λ)y + (1 + 3λ)z + 6 + 5λ=0 (2)

Now plane passes through (0,0,0) then it must satisfy the plane equation,

(1 + λ).0 + (-3 + 2λ).0 + (1 + 3λ).0 + 6 + 5λ=0

5λ=-6

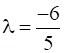
Putting in equation (2)

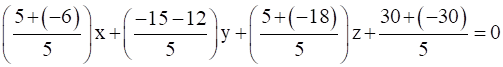
-x-27y-13z=0

x + 27y + 13z=0

So, required equation of plane is x + 27y + 13z=0.